Classroom organisation

Try to set up a stimulating physical and social environment which stimulates enjoyment and encourages learning.

Ten ways that will help motivate children to enjoy mathematics

1. Show children that mathematics is used in everyday life and problem solving.
2. Use the local environment to provide real and hands-on situations.
3. Use play to promote learning, and use games to reinforce skills.
4. Organise classes into small groups to allow individual children to share experiences.
5. Make sure that mathematics is taught as a practical subject.
6. Give time for children to discover the pattern of mathematics for themselves.
7. Do not teach formal operations until children have experienced concrete processes.
8. Remember that older children still need concrete examples and activities.
9. Show that examinations will be easier if children have good mathematical foundations.
10. Use plenty of no-cost materials for a hands-on approach to mathematics.

Classroom preparation

Arranging the physical environment

A classroom should provide stimulus and interest for mathematical thinking. For example an Interest Table could display some natural objects that lead to mathematical investigations (i.e. some honey comb showing hexagonal cells); posters and charts could pose problems; puzzles could be available such as tangrams; graphs and diagrams could stimulate thought; games could be available at all times, etc.
A less formal classroom arrangement allows for group work and more mathematical interaction. It also provides stimulation and a greater flexibility for investigations, discussions, problem solving, activity work and games.
In the two classrooms below, the small desks or tables have been pushed together to give a larger working area to help establish these ambitions:

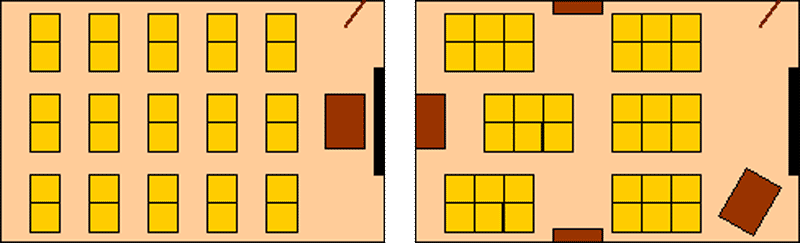
The second classroom makes it easier for group work and small discussion units. Pupils are encouraged to talk about their mathematics, and to share ideas. Group co-operation helps the teaching and learning process.

Classroom resources

Resources and classroom materials should be readily available for children to use without having to bother the teacher. Teachers complain that they have no resources but, for mathematics, most resources are free. Here is a list to help you and the children collect a Resource Bank either for your own classroom or for the whole school:

• Stones, sticks, bottle tops, shells, matchboxes, seeds, beads, nails, buttons.
• Paper, off-cuts of card, newspaper, card from boxes, old exercise books.
• Old magazines, calendars, adverts, photographs from newspapers.
• Bits of wood, bark, sticks, cubes, off-cuts.
• Bottles, plastic cups and jars, spoons, saucers, plates, tins.
• String, cotton, straw, wire, metal strips.

Apparatus, such as geoboards, tangrams, measuring tapes, metre sticks, cardboard shapes, circle makers, dice, straight edges, can be made by older pupils. A class monitor should be appointed to look after the class materials and small library.

Display areas

A mathematical display can play an important role in a classroom, and can fill a variety of functions:

• It communicates to the children in the classroom and to visitors what sort of mathematics is valued. It demonstrates the kind of mathematics that is important in the class and shows the sort of work the children have done.
• It can teach, provide information, give instructions and influence attitudes.
• It can help to motivate other children to participate in particular pieces of mathematical work that is going on in the class.
• It will help the children, who are making the displays, improve their communication skills and give them a sense of pride and achievement in the work they have done.

Encouraging co-operative learning

Children learn mathematics best if they can share ideas with others, discuss their thoughts and hypotheses, argue about things that seem wrong and reach a mutually satisfactory conclusion. It is important to give children opportunities to work together in different groupings; with friends, in mixedability groups, in similar ability groups, in large groups, in pairs, in single sex groups, and so on, in order that they may develop their skills by ‘talking through mathematics.’ They will also need to change their own role within the groups, sometimes teacher, sometimes learner, leader, follower, challenger, initiator, observer, etc.

Children value and respect each other's ideas

By your example you must show each child in the class that you value their ideas, thoughts and answers. Children, in turn, will respect the opinions and thoughts that are expressed by their peers. A teacher must be careful not to squash any ideas that are put forward or else children will be discouraged and remain silent for the rest of their school career.

The teacher should intervene when children are disrespectful to each other or laugh at the answers of others. Make sure that your children can challenge the ideas of others without making personal insults. All teachers should be aware of gender issues especially in mathematics activities where, in the past, girls have been made to feel that mathematics is ‘not their subject’. Make sure that the girls in your classes are respected and listened to as much as the boys. Mathematics is not a boys-only subject and girls can more than hold their own with boys in the right environment.

Sharing materials

The groups help in the sharing out of materials which are in short supply. The group can get closer to a single piece of apparatus, such as a thermometer. Normally the teacher has to hold this up at the front of the class and show how it works. By sharing the thermometer, with each group, for five minutes, allows all the pupils to get a closer view.

Providing a balance of mathematical activities

However good your scheme of work you will always find gaps that need filling with additional relevant activities. You have to look for a balance between:

• Work in different mathematical areas - number measurement, geometry and graphs.
• Problem solving as a mathematical exercise or everyday problem solving.
• Practice of known skills and new investigations.
• Activities which involve talking and listening, reading and recording.
• Short activities, those of medium length and longer projects.

Providing open-ended activities

You often need to provide some mathematical activities that give many possibilities. From the same starting point children can go along many different paths and perhaps ending up in different places.
These sort of activities are important for a number of reasons:

• Children can work at their own level and take the mathematics as far as their own understanding will allow.
• Children can work together to discuss their results and discoveries. This will enable them to see other ways of doing the same problem and so enrich their own understanding.
• Children learn how to use their own strategies for solving problems and compare their strategies and outcomes with others.

Working from children's own interests

Children learn best when they are absorbed in a particular activity and this is more likely if they work on tasks that arise from their own interests. Find out what your children like whether it is sports, animals, the weather, themselves, particular news items, nature, science, etc. Build on these interests with your mathematical problems.

You can also build on questions or comments made by the children. These may arise from something you have brought into the classroom and placed on the Interest Table or from a school trip or happening. Interest may be gained from a topic from another subject like geography or science.

Using mental mathematics

Children need to be able to carry out certain calculations mentally. In order to develop this skill, children will have to be able to call upon mental images and the teacher will have to consider:

• What images children see, whether it is a number ‘four’ as a numeral, or a word, or four objects in a row or in a pattern, a point on a number line or as a three and a one, etc.
• What images children have of sequences of numbers - whether they see groups of objects, a number line, numerals, words etc.
• What images children have of large numbers - whether they see a numeral or some sort of place value system.
• What mental calculations do children make - are they like they would do on paper or do they use some other way?

If children have had a firm background of manipulating apparatus when dealing with numbers, they will come to manipulate numbers mentally without difficulty. The foundation for mental work is sound addition and multiplication number bonds, together with a good grasp of place value. Often children can practice their mental agility through the use of games where pencil and paper would be inappropriate.

When and how to help children

A teacher must not spoon feed children. They must be allowed to have time to tackle problems for themselves - this is how they learn. Many children just sit and wait for the teachers help which will surely come if they wait long enough. This sort of atmosphere in a mathematics class should not be tolerated. The teacher's role is to allow children to discuss a problem and to make sure the materials for solving it are at hand. Deciding what needs to be done and how to do it is an important part of mathematical development - if the children have all this done for them they will never learn to tackle a problem for their selves. This sort of responsibility must start at an early age and as the children get older the range of situations where they take responsibility is increased.

At a certain stage your children may need a particular skill in order to work out a problem or they may need knowledge of a certain method of collecting data. At this time the teacher will teach a group that skill in order that they may go back to the problem with sufficient skills and information.

Using textbooks

The advantage of using textbooks is that they give an overall structure to the work and help inexperienced teachers with ideas and activities. Often the Teacher's Manual is more useful than the textbook because it allows some choice but still has some progression and development.

There are disadvantages to such schemes, so they should be used with care. All textbooks are rather divorced from the children's own classroom environment, interests and experiences. One way of using these books is to take single pages from it and see how you can extend the work through other activities, games, puzzles and investigations.

Classroom teaching

Introduction

Teaching concerns interaction with the children, not lecturing from the front of the class. Thought has to be given to both the children's and your own time and speed of working. Good teaching depends on good preparation, and should be relaxed and unpressured. Teaching is about what happens at the instant - what children think, say and do, and what you think, say and do as a consequence. You should be concerned with the immediate questions resulting from what the children are learning and from what they are doing. Your interactions need on the spot assessments and decisions about whether and how to intervene, and how an activity might develop. Sometimes the development of a lesson is different than that planned, if better lines of enquiry are opened up.

Your role as a teacher is to help with children's learning and to stimulate their thinking. Many teachers do not observe their children enough. Step back and see how they can work by themselves. You will be surprised. Of course you have to give them stimulating things to do. Once you have done this you must allow them to sort things out for themselves and make judgements on their own work. Too often children look at the teacher's face to see if they are wrong or right. You have to show an interest in what the children are doing but be impassive so that children will speak their own minds rather than to please you. Give encouragement but try not to show agreement or disagreement, approval or disapproval to any response.

Stimulating children's thinking

Children enjoy a challenge over a mathematical investigation. They like to put things in order, search for patterns and to try to understand. When children are doing these activities, the teacher can help to give further stimulation by asking certain types of questions. For example, let us take a lesson from the Unit on ‘Shapes – Polyominoes’:

Can you arrange these five squares in any other ways? How many ways can you find?
The children will need to think of some system of arranging and recording the squares so as to solve the problem. They will need to compare their patterns to see if they have made new arrangements or not. After some little time the teacher will come to the group and ask a few more questions to give further stimulation:

How can you be sure that you have found all the shapes possible? Are any of the arrangements the same as the others?

These questions allow children the opportunity to think further about the relationships involved in the investigations they are doing.

Making mistakes

Children learn by making mistakes. Too many teachers expect children to get the right answer after the first attempt. If teachers expect only ‘standard’ and ‘correct’ procedures in their mathematics where there is only one answer which has to be "right", then the children's thinking will be impaired. They will seek the answers that teacher wants and not throw themselves into a problem with any enthusiasm which develops into a learning situation. In a way, teachers should welcome mistakes as this allows the children to rethink a situation which, in itself, is a learning one.

Give children responsibility for their own learning

Given encouragement, children are often capable of deciding what to do next in mathematical problems and how to do it. A teacher should try to turn a question from a child back onto themselves:
Child: ‘Is this pattern the same as this one?’
Teacher: ‘What do you think?’

Classroom evaluation

Introduction

Evaluation is very much a part of teaching, involving you in making continuous observations of the children and forming intuitive judgements about them. The more formal assessment of your children's abilities will help you determine what the children's needs are, what your own needs are, and what to do in your next preparation and teaching.

Observing children

A teacher must allow time to watch the children work and listen to what they are saying. What you see and hear will help you to plan your future work. It is a good idea to have some general framework of questions to help in assessing work of any sort:

• What things are the children already confident about? Is it possible to build on these things?
• What are the children not confident with? What will I need to provide to give them a foundation to build on?
• What are the children almost grasping? What experiences do I have to provide to broaden and consolidate their knowledge, skills and understanding?

You will, of course, need to assess your own teaching and how effective it has been. Ask yourself the following questions:

• What did I set out to do?
• What did I actually achieve?
• Did it achieve what I intended?
• What did I learn?
• What would I do next time?
• Would I do the same next time?
• What will I do now?

Keeping records

It is important to keep records of children's progress, samples of their work, notes about observations and test scores. You can refer to these when you are planning. Communication with other teachers is important for ensuring continuity. As children move from class to class these records become very important.

Testing

A lot of valuable teaching and learning time can be given over to tests. It has been found that children do not learn by doing tests, especially when these tests are not followed up by careful diagnostic and remedial work. The only children who like tests are those that are successful and these children do not need them. Children learn through interest not by being faced with a test every Friday.

Who do we test?

1. The children.
2. The teacher.
3. The programme (syllabus, schemes, methods, etc.).

How do we test?

1. By questions during the lesson.
2. By regular mental tests.
3. By listening and assessing through answers.
4. By watching activities.
5. By quizzes and informal competitions.
6. By occasional formal testing.

Why do we test?

1. To see if children have learned anything during the lessons.
2. To evaluate our own teaching and methods.
3. To check the level of what we have taught.
4. To diagnose areas of difficulty.
5. To motivate children to gain better marks and to show what they can do.